|
The thought experiment which the founding 1905
paper [1] of Einstein's theory of relativity is based on concerns
a rigid rod with ends A and B, moving in the stationary system K
at velocity v parallel to the x-axis (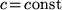 is the velocity of light):
is the velocity of light):
"Let
a ray of light depart from A at the time 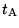 ,
let it be reflected at B at the time ,
let it be reflected at B at the time 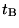 ,
and reach A again at the time ,
and reach A again at the time 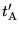 .
Taking into consideration the principle of the constancy of the
velocity of light we find that .
Taking into consideration the principle of the constancy of the
velocity of light we find that
and
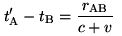
(click
on the formula to see derivaltion)
where
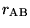 denotes the length of the moving rod
-- measured in the stationary system."
denotes the length of the moving rod
-- measured in the stationary system."
The
first of the above formulae expresses
the time
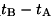 necessary for the light to
travel from A to B, measured by the
clocks in K where end A and end B of
the rigid rod happen to be in K, while
the second expresses the time
necessary for the light to
travel from A to B, measured by the
clocks in K where end A and end B of
the rigid rod happen to be in K, while
the second expresses the time 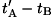 necessary for the light to travel from
B back to A, again, measured by the
clocks placed where ends A and B happen
to be in K.
necessary for the light to travel from
B back to A, again, measured by the
clocks placed where ends A and B happen
to be in K.
It cannot be emphasized stronger that
the above formulae are derived by the
stationary observers (observers in K)
for the purposes of drawing a conclusion
as to what the observers moving with
the rod (observers in k) see. Since
the observers in K have at their disposal
only the parameters of the stationary
system K, Einstein needed an additional
rule which would allow the observers
in K to become speakers for the observers
in k:
To solve the contradiction between the
fact that the indications of the clocks
participating in the above inequality
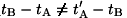 (undoubtedly,
therefore, an inequality derived in
the stationary system K), are
indications of clocks in the stationary
system K, while for the purposes of
his conclusion these quantities have
to be indications of clocks also in
the moving system k, Einstein
spells out explicitly the following
obvious rule for the connection between
the readings of clocks in the stationary
system K and the readings of the clocks
in the moving system k spatially
coinciding with them (rule
for the synchronicity in K of spatially
coinciding clocks):
(undoubtedly,
therefore, an inequality derived in
the stationary system K), are
indications of clocks in the stationary
system K, while for the purposes of
his conclusion these quantities have
to be indications of clocks also in
the moving system k, Einstein
spells out explicitly the following
obvious rule for the connection between
the readings of clocks in the stationary
system K and the readings of the clocks
in the moving system k spatially
coinciding with them (rule
for the synchronicity in K of spatially
coinciding clocks):
"We
imagine further that at the two ends
A and B of the rod, clocks are placed
which synchronize with the clocks of
the stationary system, that is to say
that their indications correspond at
any instant to the "time of the
stationary system'' at the places where
they happen to be. These clocks are
therefore "synchronous in the stationary
system"."
Having done that, Einstein now takes
advantage of the obvious, while foisting
on the reader the universality of 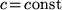 ,
that the clocks placed at A and B (at
rest with k) would be synchronous, that
is, would have common time in
the moving system k if and only if the
above times ,
that the clocks placed at A and B (at
rest with k) would be synchronous, that
is, would have common time in
the moving system k if and only if the
above times 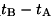 and
and 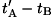 obeyed the following definition for
synchronicity given in §1 of the 1905
paper:
obeyed the following definition for
synchronicity given in §1 of the 1905
paper:
"... the "time'' required
by light to travel from A to B equals
the "time'' it requires to travel
from B to A. "
However, as follows purely formally
from the above formulae, under the foisted
condition for the velocity of light
being always 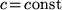 also in k, that it is not so in k. On
the contrary, as is seen, what follows
from the above formulae
also in k, that it is not so in k. On
the contrary, as is seen, what follows
from the above formulae 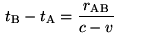 and
and
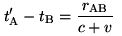 ,
provided the velocity of light is under
any circumstances ,
provided the velocity of light is under
any circumstances 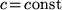 ,
the purported relationship in k is always
the inequality ,
the purported relationship in k is always
the inequality
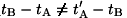
This inequality
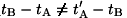 ,
derived,
as said, in the stationary system
K but transferred according to the above
rule for the synchronicity in K of spatially
coinciding clocks into the moving
system k, together with ,
derived,
as said, in the stationary system
K but transferred according to the above
rule for the synchronicity in K of spatially
coinciding clocks into the moving
system k, together with 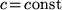 in
k, is, according to Einstein, the proof
that the clocks at A and B in the moving
system k do not have common time, that
is, that:
"Observers
moving with the moving rod would thus
find that the two clocks were not synchronous".
Once
again, this is so because,
obviously, in order for the clocks in
question to have common time when
in
k, is, according to Einstein, the proof
that the clocks at A and B in the moving
system k do not have common time, that
is, that:
"Observers
moving with the moving rod would thus
find that the two clocks were not synchronous".
Once
again, this is so because,
obviously, in order for the clocks in
question to have common time when 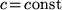 ,
they have to obey the following, already
mentioned, evident criterion for synchronicity,
given in §1 of the 1905
paper: ,
they have to obey the following, already
mentioned, evident criterion for synchronicity,
given in §1 of the 1905
paper:
"... the "time'' required
by light to travel from A to B equals
the "time'' it requires to travel
from B to A. "
which is a criterion clearly not obeyed
by the above-observed inequality
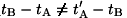 if indeed
if indeed 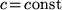 in k.
in k.
This
section is devoted to explaining what
the essence of the thought experiment
in [1]
is. Nevertheless, it is imperative to
state at once even at this point that,
of course, the above conclusion, namely,
that the clocks at A and B moving with
the rod are non-synchronous, made in
the described way, is in error.
As
can clearly be seen,
the very formulae 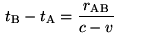 and
and
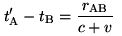 Einstein
uses to prove such non-synchronicity
in fact prove conclusively that the
clocks in question are, in fact, nothing
but synchronous.
Einstein
uses to prove such non-synchronicity
in fact prove conclusively that the
clocks in question are, in fact, nothing
but synchronous.
The above erroneous conclusion for the
non-synchronicity of the clocks at A
and B in k can only be arrived at if
one "forgets" the obvious
truth that the clocks at A and B are
nothing but synchronous (the latter
follows
directly
from the very formulae Einstein presents
in §2 of
[1]),
and one only decides to give credence
to the joint validity of the only possible
relationship between times 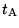 , ,
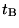 and
and 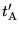 in k, namely, the inequality
in k, namely, the inequality
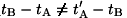 on
the one hand and on the other the equality
on
the one hand and on the other the equality
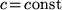 ,
pronounced to be the universal velocity
of light in any system, including k.
Such "forgetting" of the truth
and forging imposed conditions so that
it would appear that one proves one's
point is clearly a completely unacceptable
manipulation which has no place in any
logical discourse let alone in a discourse
in science. ,
pronounced to be the universal velocity
of light in any system, including k.
Such "forgetting" of the truth
and forging imposed conditions so that
it would appear that one proves one's
point is clearly a completely unacceptable
manipulation which has no place in any
logical discourse let alone in a discourse
in science.
On the other hand, for 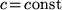 ,
for a rigid rod at rest with the stationary
system K, the valid relationship for
the observers in K (observers at rest
with the rod) is obviously the equality ,
for a rigid rod at rest with the stationary
system K, the valid relationship for
the observers in K (observers at rest
with the rod) is obviously the equality
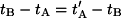 ,
which according to the above definition
is the basis to assert, as Einstein
correctly does, that the clocks at A
and B of the rigid rod, immovable with
respect to K, do have common time and
are synchronous, that is, to
state that "while observers
in the stationary system would declare
the clocks to be synchronous." ,
which according to the above definition
is the basis to assert, as Einstein
correctly does, that the clocks at A
and B of the rigid rod, immovable with
respect to K, do have common time and
are synchronous, that is, to
state that "while observers
in the stationary system would declare
the clocks to be synchronous."
Based on the above Einstein makes the
following (incorrect) general conclusion.
"So
we see that we cannot attach any absolute
signification to the concept of simultaneity,
but that two events which, viewed from
a system of co-ordinates, are simultaneous,
can no longer be looked upon as simultaneous
events when envisaged from a system
which is in motion relatively to that
system."
considered as one of the greatest discoveries
of all time, known under the term "relativity
of simultaneity", which underlies
anything Einstein's theory of relativity
represents.
As
explained,
the conclusion for "relativity
of simultaneity" is incorrect
and that is seen directly from the very
formulae presented by Einstein with
the aim to prove it.
One may also consider the following,
slightly modified, way of debunking
the claim for the "relativity
of simultaneity":
It is seen
at once [link][link]
that
for
a source of light at rest with the stationary
system,
the formulae 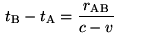 and
and 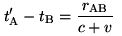 which
Einstein uses to "prove" relativity
of simultaneity are derived purely classically
(without Einstein's theory of relativity),
despite Einstein's insistence in §2
of his
1905 paper [1]. which
Einstein uses to "prove" relativity
of simultaneity are derived purely classically
(without Einstein's theory of relativity),
despite Einstein's insistence in §2
of his
1905 paper [1].
Thus, having these formulae present
in classical physics (the physics without
Einstein's theory of relativity) the
only thing needed for the relativity
of simultaneity to be claimed is to
postulate that "light
is always propagated in empty space
with a definite velocity c which
is independent of the state of motion
of the emitting body", that
is, that 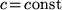 under
any circumstances (this is known as
the second postulate of Einstein's theory
of relativity; cf. the
preamble of his founding 1905 paper
[1]).
under
any circumstances (this is known as
the second postulate of Einstein's theory
of relativity; cf. the
preamble of his founding 1905 paper
[1]).
However, to postulate
that 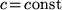 is the universal velocity of light would
be tantamount to postulating that the
clocks at ends A and B of the rod, moving
with the moving rod, are always
non-synchronous because universality
of
is the universal velocity of light would
be tantamount to postulating that the
clocks at ends A and B of the rod, moving
with the moving rod, are always
non-synchronous because universality
of 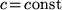 leads to the inevitable derivation of
solely the inequality
leads to the inevitable derivation of
solely the inequality 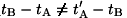 in
the moving system k
-- recall, joint
validity of the inequality
in
the moving system k
-- recall, joint
validity of the inequality 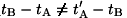 and the equality
and the equality 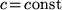 in a given system is impossible for
synchronous clocks;
only
the readings of non-synchronous clocks
can exhibit the inequality
in a given system is impossible for
synchronous clocks;
only
the readings of non-synchronous clocks
can exhibit the inequality 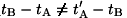 when
when 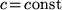 . .
However, as
seen, the very formulae Einstein
uses to "prove" non-synchronicity
of the clocks at A and B in k directly
show the opposite, namely, that these
clocks are nothing but synchronous.
As
was said above, the discussed erroneous
conclusion for "relativity of
simultaneity" can only be arrived
at if one "forgets" the obvious
truth that the clocks at A and B are
nothing but synchronous (following from
the very formulae Einstein presents
in §2 of
[1]),
and only decides to gives credence to
the joint validity of the only possible
relationship between times 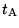 , ,
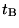 and
and 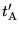 in k, namely, the inequality
in k, namely, the inequality 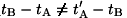 on one hand
and
on the other the equality
on one hand
and
on the other the equality 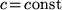 ,
pronounced to be the universal velocity
of light in any system, including k.
This "forgetting" of the truth
and forging imposed conditions with
the aim to appear that one proves one's
point is clearly a completely unacceptable
manipulation which has no place in any
logical discourse let alone a dicourse
in science. ,
pronounced to be the universal velocity
of light in any system, including k.
This "forgetting" of the truth
and forging imposed conditions with
the aim to appear that one proves one's
point is clearly a completely unacceptable
manipulation which has no place in any
logical discourse let alone a dicourse
in science.
If one needs
the above to be stated in a different
way then one
may observe
that an initial condition comprising
a postulate such as the one requiring
universality of 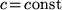 is
unfounded because it contradicts another
initial condition -- validity of Newton's
mechanics in the stationary system K.
As
seen Newton's mechanics inevitably
leads to the fact that two synchronous
clocks in one system remain synchronous
in all systems. Postulating in the same
breath universality of
is
unfounded because it contradicts another
initial condition -- validity of Newton's
mechanics in the stationary system K.
As
seen Newton's mechanics inevitably
leads to the fact that two synchronous
clocks in one system remain synchronous
in all systems. Postulating in the same
breath universality of 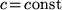 is tantamount to postulating that the
opposite is true because then, as said,
the only possible relationship between
times intervals
is tantamount to postulating that the
opposite is true because then, as said,
the only possible relationship between
times intervals 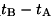 and
and 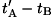 read from the faces of clocks in k is
the inequality
read from the faces of clocks in k is
the inequality 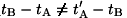 ,
which means that the only possibility
for the clocks in k when ,
which means that the only possibility
for the clocks in k when 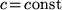 is to be non-synchronous.
This is a contradiction -- the clocks
at A and B are always synchronous but
the postulate for the universality of
is to be non-synchronous.
This is a contradiction -- the clocks
at A and B are always synchronous but
the postulate for the universality of
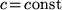 derives that they are always non-synchronous.
derives that they are always non-synchronous.
Therefore,
Einstein's inferrence that the observers
in the two different systems will arrive
at different conclusions regarding simultaneity
of one and the same pair of clocks in
one and the same system k, is nothing
else but a most common mistake and is
contradictory in itself. It is a result
of flagrant manipulation of contradictory
initial conditions.
|