It is amazing what conclusions one may arrive at when just following nothing more than most basic definitions, such as the definitions of velocity and acceleration, comprising absolute truths:



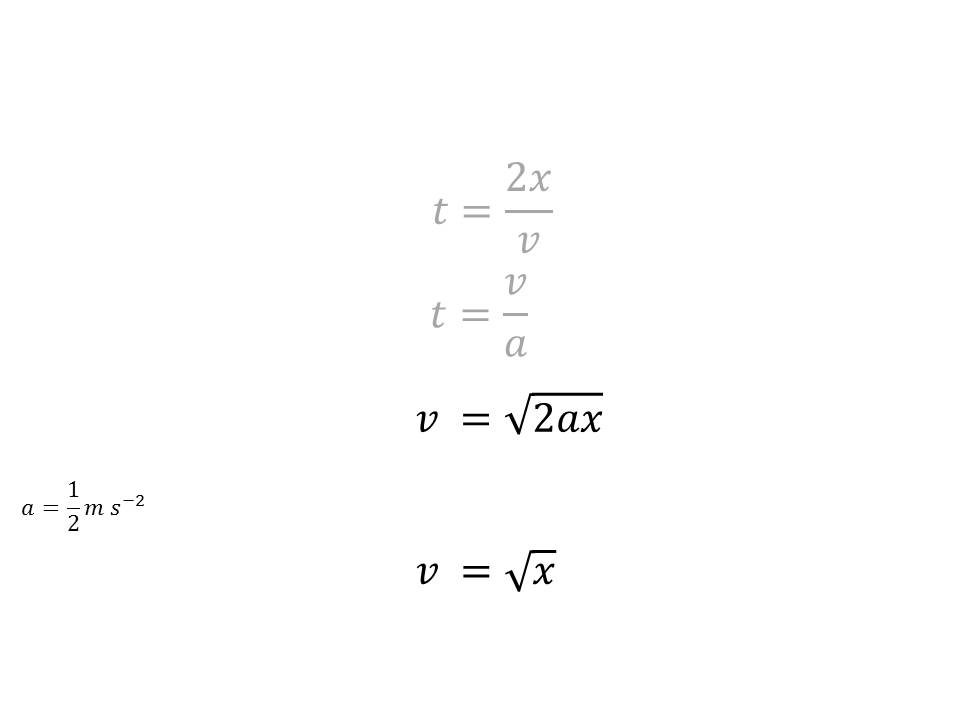
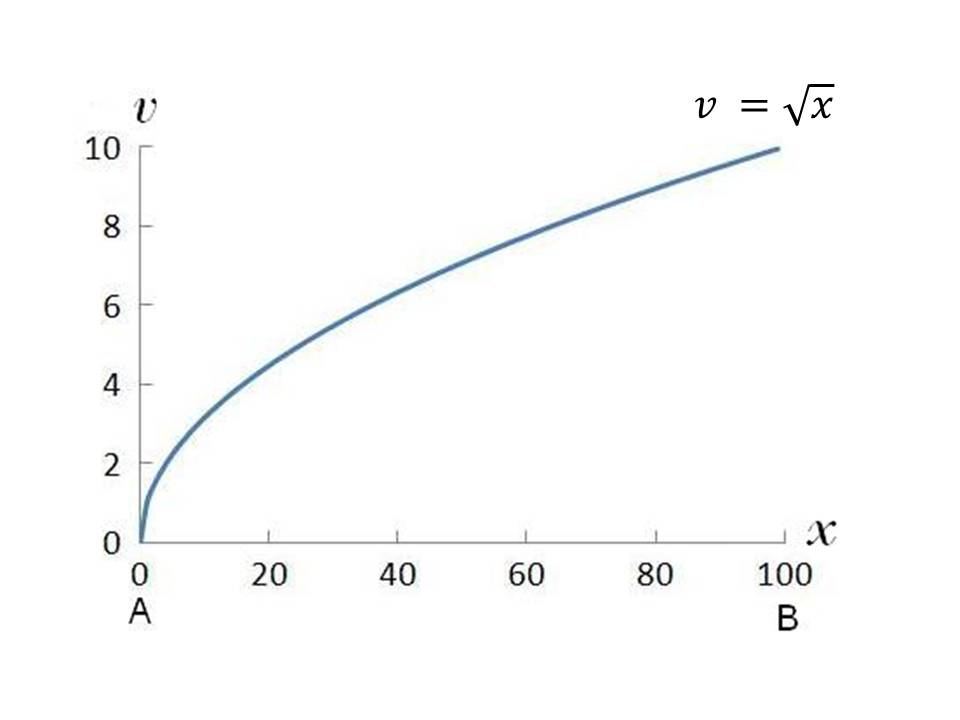
As seen from the graph, when a free body is acted upon by a constant force (maintaining constant acceleration a), velocity v of that body is tending toward a limiting value at large displacements x.

It is also amazing what conclusions one may arrive at when considering the obvious absolute fact that at the end of a non-zero real spatial shift x, resulting from the application of constant force on a real body, velocity v must necessarily be non-zero.

Considering the above, the known form of Newton's second law is clearly untenable:

As seen, Newton's second law in its known form leads to the incorrect conclusion that the work A is zero, when transporting a body, under the action of a constant force, across a non-zero distance x.

Thus, the known Newton's second law is not a law of motion, as claimed, but is a law of rest.

To become law of motion it must be corrected by honoring the fact that if there were to be a real, non-zero displacement x, then the applied force F_real must be greater than the counteracting (due to Newton's third law) force of inertia ma. This difference also causes the velocity of the body at the end of its real, non-zero, displacement to be non-zero; that is, the body to have kinetic energy . Thus, instead of the known Newton's second law, leading to the above-mentioned D'Alembert's principle, the physical meaning requires to write the following:

From the above-derived , we get , which we substitute in the above expression for the real force, to convince ourselves that . Indeed,

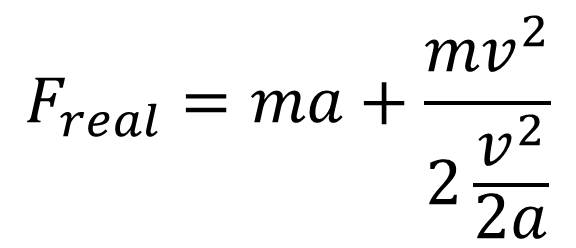
And, now we see that on the left of the equality, the quantity is nothing other than energy, while on the right of the equality the mass is multiplied by the square of the velocity, which at large displacement x is tending toward a limiting velocity c. Thus, we clearly get the mass-energy relationship E = mc², derived purely clasically.

Mass-energy relationship E = mc² is contained in Ampere’s law inherently.



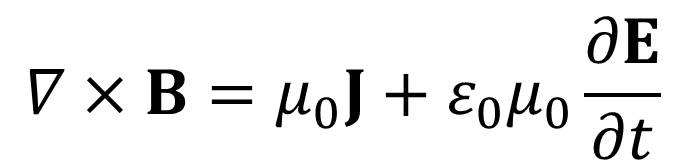
both sides of which are multiplied scalarly with the vector of the electric fieldand using the equality



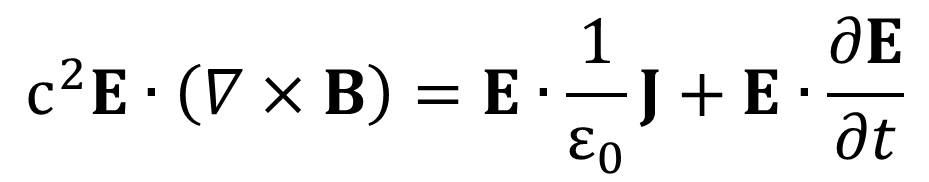
Now, we can carry out dimensional analysis of the above equation, equivalent to Ampere's law.

The dimensions of the left side of the equation are , which is

As expected, the dimensions of the two terms on the right side of the equation are the same

Indeed, the first term on the right is , while the second term on the right is . Thus, we get